Computer Science Note - Data structure
Data Structure
Array
We are all know and familiar with Array, so I don't write much about this data structure. Below is just an example of Array and the Big O time
Example 1:
1def foo():
2 sum = 0
3 product = 1
4 for i in [0:n]:
5 sum += i
6 for i in [0:n]:
7 product *= i
The above example actually loop array twice, it took O(2N) time. However, 2 is a constant and has no big deal with total runtime if N increase. So, the Big O time is O(N)
Example 2:
1def foo():
2 sum = 0
3 product = 1
4 for i in [0:n]:
5 sum += i
6 for i in [0:m]:
7 product *= i
You can see that above example loop two different array with O(NM) time. We don't know any relation between N and M, so we can NOT drop O(M).
Hash Tables
A hash table is a data structure that maps keys to values for highly efficient lookup. There are many ways to implementing this. But I used an array of linked list and a hash code function.
- First, compute key's hash code.
- Then, map the hash code to an index in the array.
- At the index, we use a
Linked Listof key and values. Because there are diferrent keys have the same hash code and index.
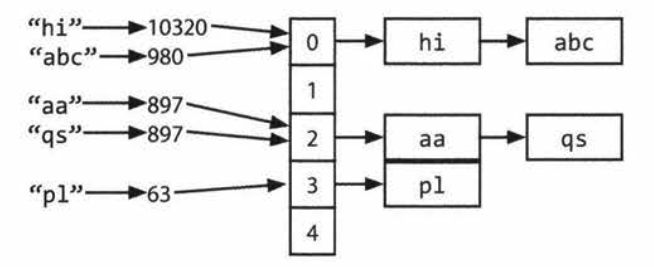
To retreive value from the key, we do the following steps:
- Compute the hash code from the key.
- Compute the index from the hash code.
- From index, search through the linked list for get the value of this key.
Time Complexity (Big O)
- Search:
O(1)- Compute hash code from key took O(1)
- Compute index from hash code took O(1)
- Search through linked list took O(1) in
average. We assume that not all key of hash table have the same index. - In
worst case, if all the keys of hash table have the same index, search through linked list must took0(n)time.
- Insertion:
O(1)- Worst case:
O(n)
- Worst case:
- Deletion:
O(1)- Worst case:
O(n)
- Worst case:
Implementation
1class Item(object):
2 def __init__(self, key, value):
3 self.key = key
4 self.value = value
5
6class HashTable(object):
7 def __init__(self, size):
8 self.size = size
9 self.table = [[] for _ in range(self.size)]
10
11 def _hash(self, key):
12 # Use can use any logic here to create a hash code for the given key
13 return key % self.size
14
15 def set(self, key, value):
16 hash_index = self._hash(key)
17 for item in self.table[hash_index]:
18 if item.key == key:
19 item.value = value
20 return
21 self.table[hash_index].append(Item(key, value))
22
23 def get(self, key):
24 hash_index = self._hash(key)
25 for item in self.table[hash_index]:
26 if item.key == key:
27 return item.value
28 raise KeyError('Key not found')
29
30 def remove(self, key):
31 hash_index = self._hash(key)
32 for index, item in enumerate(self.table[hash_index]):
33 if item.key == key:
34 del self.table[hash_index][index]
35 return
36 raise KeyError('Key not found')
See detail from here
Linked List
A linked list is a data structure that represents a sequence of nodes. In a singly linked list, each node pointed to the next node in the linked list. A doubly linked list gives each node pointers to both of next node and the previous node.
The following describe a doubly linked list:
1..... --> ..... --> ..... --> .....
2. 1 . . 2 . . 3 . . 4 .
3..... <-- ..... <-- ..... <-- .....
Time Complexity (Big O)
- Access:
O(n) - Insertion:
O(n)O(1)if you hold the trail pointer
- Deletion:
O(n)O(1)if you know the pointer need to be deleted
Implementation
Here is simply implementation of singly linked list
1class Node(object):
2 def __init__(self, data):
3 self.next = None
4 self.data = data
5
6# Singly Linked List
7class LinkedList(object):
8 def __init__(self):
9 self.head = None
10
11 def add(self, data):
12 end = Node(data)
13 if self.head == None:
14 self.head = end
15 return
16
17 # Traveling through linked list to find trail of list
18 n = self.head
19 while n.next != None:
20 n = n.next
21 n.next = end
22
23 def remove(self, data):
24 n = self.head
25 prev = self.head
26 while n.next != None:
27 if n.data == data:
28 prev.next = n.next
29 return
30 else:
31 prev = n
32 n = n.next
33 raise KeyError('Data not found')
34
35 def show(self):
36 n = self.head
37 while n != None:
38 print(n.data)
39 n = n.next
See detail from here
Stack
A Stack uses LIFO (Last in first out) ordering. It use the following operations.
- pop ( ) : Remove the top item from the stack.
- push ( i tern): Add an item to the top of the stack.
- peek ( ) : Return the top of the stack.
- is Empty ( ) : Return true if and only if the stack is empty.
Time complexity
- Access:
O(n) - Search:
O(n) - Insertion:
O(1) - Deletion:
O(1)
Implementation
Here is an example of implementation Stack by Python.
1class Node(object):
2 def __init__(self, data):
3 self.next = None
4 self.data = data
5
6class Stack(object):
7 def __init__(self):
8 self.top = None
9
10 def push(self, data):
11 n = Node(data)
12 if self.top == None:
13 self.top = n
14 else:
15 n.next = self.top
16 # Change the added node to top of stack
17 self.top = n
18
19 def pop(self):
20 if self.top == None:
21 raise KeyError('Stack is empty')
22 n = self.top
23 self.top = self.top.next
24 return n.data
See more detail from stack.py